Le modèle logistique (Verhulst 1836) est utilisé comme modèle en dynamique des populations. Il répond aux exigences suivantes :

• les ressources étant limitées, la population ne peut pas croître indéfiniment
• si la population devient trop importante et manque de ressources, elle doit diminuer

Une solution pour modéliser ce phénomène est d'utiliser l'équation discrète suivante (équation logistique) : $$N(t+1)=f(N(t))=rN(t)\left(1-\frac{N(t)}{K}\right)$$ Les paramètres $r$ et $K$ permettent d'influer sur :

• la tendance à la surpopulation
• la quantité de ressources disponibles, autrement dit la taille maximale de la population

L'équation logistique est très simple et permet de calculer très facilement une estimation de la population en fonction de la taille de la population l'an passé (par exemple), dans le cas simple d'un milieu à ressources limitées mais ne contenant qu'une espèce (pas de prédation).

Malgré cette apparente simplicité, l'étude de la stabilité de la population à long terme peut s'avérer surprenante. Plus particulièrement, nous allons nous demander si la population tend vers une valeur stable, oscille autour de deux valeurs ou autour de plusieurs valeurs.

Ces simulations seront réalisées avec Octave (ou Scilab, ou Matlba), et afin de pouvoir utiliser d'autres modèle que le modèle logistique, nous allons écrire des fonctions très générales.

Écrivez tout d'abord une fonction, nommée modelelogistique qui prend en paramètre N(t) et un vecteur contenant les deux paramètres de l'équation logistique (r et K), et renvoie N(t+1).

Testez votre fonction pour r=0.3, N(t)=500 et K=1000 :

modelelogistique(500,[0.3 1000])
=> 75

Nous allons à présent écrire une fonction qui renverra deux vecteurs décrivant l'évolution de la population d'année en année. Cette fonction s'appellera histoire, et prendra en paramètre :

• la population initiale
• le nombre d'années de simulation
• la fonction qui modélise notre écosystème
• les paramètres utiles à la fonction précédente

Notez que la fonction histoire est une fonction qui prend une autre fonction en paramètres.

Testez votre fonction ainsi :

[t,y]=histoire(500,100,@modelelogistique,[2.7 1000]);
plot(t,y)

Notez au passage comment envoyer une fonction en paramètre (la notation @ est spécifique à Matlab et Octave, avec Scilab, il faut supprimer le @). Essayez aussi de tracer en utilisant plot(t,y,'.').

Vous devez obtenir un graphique comme celui-ci :

On constate qu'en une quinzaine d'année, la population s'est stabilisée à environ 630 individus.

Il est évidement très facile d'obtenir une nouvelle simulation en changeant le paramètre $r$ de l'équation de départ. Qu'obtenez vous pour $r=3.1$ ?

Ce n'est que lors de l'apparition des premiers ordinateurs qu'on a pu facilement explorer de façon systématique l'influence du paramètre $r$ sur le comportement qualitatif de la taille de la population.

On peut par exemple obtenir une “periode” égale à 3 en utilisant $r=3.835$ (pour le voir, il faudra tracer les points obtenus sans les relier par des points, en écrivant quelque chose comme : plot(t,y,'.') ).

Comment représenter l'influence de $r$ sur le comportement de la taille de la population ? On cherche à savoir, au bout d'un certain temps, si la population est stabilisée sur une valeur (et si oui laquelle), si elle oscille entre deux valeurs, et si oui lesquelles, entre 3 valeurs, ou encore si elle a un comportement qui semble être chaotique comme pour $r=3.655$.

Cette représentation que nous allons à présent tracer s'appelle un diagramme de bifurcations. Nous placerons en abscisse le paramètre $r$ et en ordonnée les valeurs de population atteintes “au bout d'un certain temps”.

Ainsi, notre première observation conduit au tracé du point (2.7 629.2). La seconde observation, que vous avez faite, devrait vous conduite à tracer les deux points (3.1, 764.56) et (3.1,558.014).

Nous devons réaliser ce tracé automatiquement.

Diagramme de bifurcation de la fonction logistique

Pour cela, nous allons utiliser la fonction histoire, en lui indiquant une valeur $r$, et lui demander de calculer la population sur 60 ans (par exemple). Puis nous prendrons tous les points obtenus pour les abscisses de 50 à 60 (par exemple) et les placerons sur le diagramme de bifurcation à l'abscisse $r$.

Pour $r=2.7$, nous aurons donc 11 points (presque) confondus. Pour $r=3.1$ nous aurons deux “paquets” de points etc…

La fonction bifurcations que nous allons écrire devra prendre en paramètres :

• le modèle du système
• la valeur de la population initiale
• les dates min et max de points retenus (50 et 60 dans notre exemple).
• le vecteur paramètre par défaut
• le numéro du paramètre qui doit figurer en abcisse
• un vecteur contenant les valeurs prises par ce paramètre

La fonction devra renvoyer les paires de coordonnées des points figurant dans le diagramme :

vals=bifurcations(500,50,60,@modelelogistique,[2.5 1000],1,[2.5:0.001:4]);
plot(vals(:,1),vals(:,2),'.');

Bien sûr, il faut ici tracer les points sans les relier. Pour obtenir un graphique plus précis, il faut diminuer la taille des points tracés. Ceci se fait différemment sous Matlab ou Scilab.

Le diagramme obtenu permet de relever à quel moment ont lieu les doublements de période. Il est possible de zoomer sur ce graphique, puis d'en obtenir un plus précis en relançant la fonction bifurcation avec de nouvelles bornes.

On peut de cette façon remarquer la nature fractale du diagramme de bifurcations de l'application logistique. Pour vous en convaincre, tracez le diagramme pour $3.84\leq r \leq 3.86$. Vous devez obtenir trois zones distinctes. Zoommez avec le zoom Matlab dans la partie inférieure. La zone que vous obtenez sera un agrandissement de la zone indiquée sur l'image suivante.

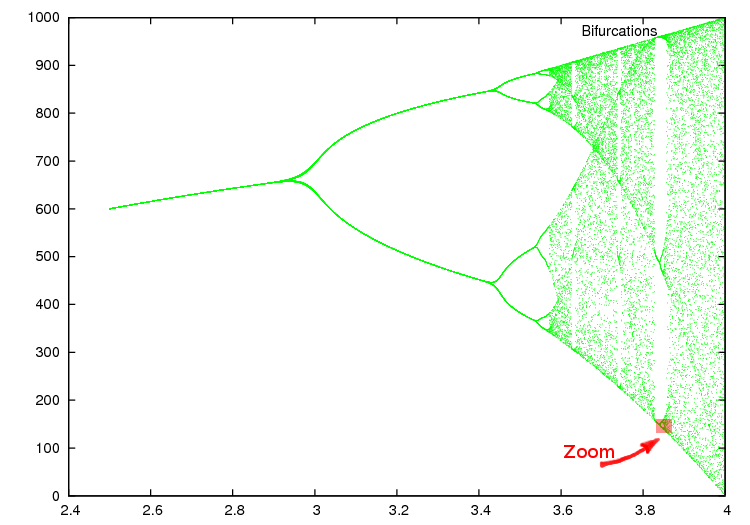
Sur ce nouveau diagramme, regardez ce qui se passe pour $r \approx 3.854$… le processus peut ainsi être répété à l'infini.

Vous devez rendre un rapport contenant :

• le texte de vos fonctions ;
• un exemple de leur utilisation ;
• les courbes obtenues ;
• vos commentaires éventuels.