Outils pour utilisateurs
Table des matières
📓 Propagation d'une épidémie
Dans ce TP, nous proposons de programmer un simulateur permettant d'observer la manière dont une épidémie se répand.

Avant de commencer la lecture du sujet, vous devez prendre connaissance de la manière de programmer un automate cellulaire en 2D. Ce point est abordé sur la page [[stu:python:automates_cellulaires_2d|Automates cellulaires 2D : Généralités]]. Vous aurez peut être aussi besoin de vous renseigner sur les [[stu:python_gui:pygame|Graphismes en Python]]
Références
États des cellules
Les cellules peuvent être dans un des cinq états suivants : Vide1), Mort, Sain, Immunisé, Malade
Règles de transition
Les règles de transition sont :
- Une cellule Morte reste Morte
- Une cellule Malade devient Morte avec une probabilité p1 ou Immunisée avec une probabilité (1-p1)
- Une cellule Immunisée reste Immunisée
- Une cellule Saine
- devient Malade si elle a un voisin Malade avec une probabilité p2
- reste Saine sinon
Le voisinage considéré est un voisinage de Moore (8 voisins).
Programmation
Des instructions sur la manière de procéder et sur l'ordre dans lequel créer ce programme sont données dans la documentation générale sur les automates 2D.
Les valeurs de p1 et p2 doivent pouvoir varier pour réaliser tous les tests suggérés dans la suite du TP. Pensez-y dès le début.
Spécificités de cet automate
- Pour cette simulation, il est préférable d'initialiser toutes les cellules du tableau dans l'état Sain sauf une dans l'état Malade
- Il est utile de mettre les deux probabilités p1 et p2 en paramètre de la fonction
suivant - Pour détecter la fin d'une simulation, on peut apporter une modification à
suivant: un flag est mis àTrueen début de procédure, puis, si un état change, il passe àFalse. S'il est encore àTrueen fin de procédure, c'est que l'état est stable. On pourra par exemple modifiersuivantpour qu'elle retourne ce flag, indiquant ainsi si la simulation est terminée ou non. - Vous devrez réaliser une fonction qui comptabilise le pourcentage de cellules dans chaque état. Pensez à utiliser des dictionnaires.
- Dans la suite, vous êtes amenés à apporter des modifications : attention à ce que vos fonctions ne deviennent pas trop longues ou compliquées, suite à des modifications
Ne pas hésiter à remettre en question son travail et à en reprendre une partie pour la coder plus proprement. Le temps passé à faire ça est du temps gagné par la suite.
À quoi utiliser l'automate
Outre l'activité purement contemplative qui consiste à observer les changements d'états des cellules, cet automate est adapté à une étude statistique. Pour cela, vous devez pourvoir lancer plusieurs simulations (une simulation s'arrête lorsque l'automate n'évolue plus). Dans le cas de chaque simulation, comptabilisez les nombre de cellules qui sont restées saines, sont immunisées ou sont mortes. En réalisant des moyennes sur quelques dizaines de tests, vous pouvez alors mesurer le comportement moyen de l'automate, en fonction des paramètres p1 et/ou p2.
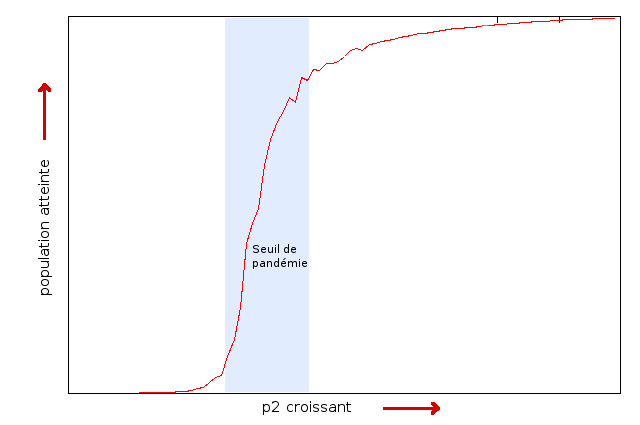
Pour p1 fixé à 0.5, à partir de quelle valeur de p2 avons nous affaire à une pandémie (c'est à dire à une contamination généralisée) ? Pour faire ce calcul vous pourrez comptabiliser le nombre de cellules mortes ou immunisées à la fin de la simulation (mais il y a d'autres moyens de procéder, si vous avez une autre idée, n'hésitez pas à la programmer) et contrôler comment varie cette valeur en fonction de p2 (voir la courbe ci-dessous)
Si on immunise (par un vaccin) 25 % des cellules dès le début (à l'initialisation), quelle est le nouveau seuil critique pour p2 ? Il vous faudra sans doute différencier les individus immunisés par vaccin de ceux immunisés suite à la maladie pour comptabiliser les cellules qui ont été atteintes. Vous pourrez le faire par exemple en ajoutant un état. Il est de plus intéressant de regarder la proportion d'individus ayant été atteints par la maladie à l'interieur de la populaiton **non vaccinée**. Vous ferez ainsi apparaître que la vaccination à grande échelle a évidemment une influence sur les individus vaccinés, mais aussi sur ceux qui ne le sont pas.
Commentez les résultats que vous avez obtenus.
Quel est, à votre avis, la simplification la plus critique faite dans ce modèle (i.e. quelle propriété améliorer en premier pour le rendre plus réaliste) ? Argumentez.
Vous pouvez essayer de produire des courbes de ce genre :