Table des matières
⚠ Attracteur de Lorenz
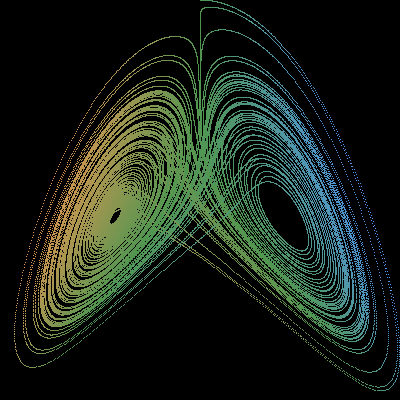
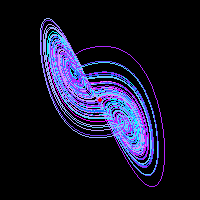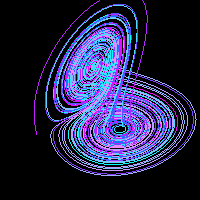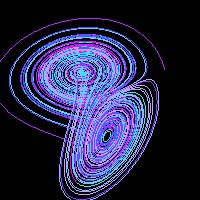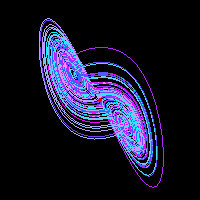
On se propose dans ce TP de simuler et de tracer l'attracteur de Lorenz, souvent utilisé pour illustrer des propos sur le chaos déterministe.
Prérequis
Références
Travail à rendre
- un fichier PDF nommé
login_lorenz.pdfcontenant votre rapport (les réponses aux question posées dans ce sujet) - le programme Python réalisé :
login_lorenz.py - Une image, au format PNG que vous avez obtenue :
login_lorenz.png
Votre programmes Python doit être automone (s'exécuter sans intervention dans le shell), mais aussi importable de manière silencieuse. Faites comme indiqué dans ce guide : Notes sur Python - Programme propre. Si vous ne comprenez pas ce point, demandez à l'encadrant.
Présentation et résolution numérique
Définition du système
L'attracteur de Lorenz est obtenu en traçant le lieu de points de l'espace qui satisfont le système d'équations différentielles suivant: $$\left\{\begin{array}{l}x^\prime=w(y-x)\\y^\prime=rx-y-xz\\z^\prime=-bz+xy\end{array}\right.$$
Dans ces équations le point M qui décrit la courbe a pour coordonnées (x,y,z) et pour vitesse (x',y',z'). Les paramètres du système dynamique sont w, b et r qu'on prend généralement égaux à 10, 8/3 et 28 pour obtenir l'image bien connue de l'attracteur.
La condition initiale pourra être un point proche de l'origine.
Expliquez pourquoi on prend comme point de départ un point proche de l'origine, mais pas l'origine.
Résolution du système
Pour résoudre le système, on pourra utiliser par exemple la méthode d'Euler. Un pas de calcul dt étant fixé (par exemple dt=0.001), on calculera les itérations suivantes :
$$M_{n+1}=M_n+dt\times M_n^\prime$$
où $M_n^\prime$ est mis pour la vitesse au point $M_n$.
Codage
Codage du système dynamique
Quelle type de données utiliser pour stocker les coordonnées $M_n$ ou la vitesse $M_n^\prime$.
Écrivez la fonction nommée vitesse qui prend en paramètre $M_n$ et renvoie $M_n^\prime$.
Les trois paramètres $b$, $w$ et $r$ seront passés à la fonction par le biais d'un dictionnaire.
Écrivez une fonction nommée calcul qui prend en paramètres dt, n, M0, le dictionnaire des paramètres et calcule n points de l'attracteur
(vous utiliserez donc la fonction nommée vitesse) en partant du point M0. Votre fonction renverra une liste ou un tuple de points.
Écrivez la fonction main qui lance calcul et affiche les coordonnées des points calculés à l'écran. Testez votre programme à la main sur quelques valeurs (les tests devront figurer dans le rapport).
Lorsque vous avez vérifié que votre programme était juste, réglez ces paramètres :
M0=(0,0.1,0)dt=0.001w=10,b=8/3,r=28n=99000
Relevez les valeurs min et max prises par chaque coordonnée. Notez ces valeurs dans votre rapport et indiquez comment les utiliser pour obtenir une figure centrée sur l'écran.
Les fonctions calcul et vitesse doivent être fonctionnelles. Vous ne devez plus les retoucher.
Si vous pensez devoir le faire, demandez l'avis de l'encadrant auparavant.
Modifiez la fonction main pour qu'elle ouvre une fenêtre et trace les points à l'écran plutôt que d'afficher leurs coordonnées.
Expliquez les choix que vous faites en ce qui concerne la projection de la figure 3D sur l'écran.
- Imaginez un moyen pour obtenir des figures systématiquement bien centrées à l'écran (vous l'implémenterez si vous avez le temps).
- Imaginez un moyen de représenter la profondeur (vous l'implémenterez si vous avez le temps).